College Women's USAU Rankings (OV)

2024-25 Season

Data updated through April 28 at 11:45pm EDT

FAQ
Division I // Division III
Rank    Change Team                                                 Record Rating Change Region Conference Div   SoS PDC %
20 3 Pennsylvania OV 1 20-8 1912.4 333 Ohio Valley Pennsylvania DI D-I 1703.25 209.17 0.12
22 1 Ohio State 22-8 1891.53 375 Ohio Valley Ohio DI D-I 1824.19 67.35 0.04
31 Pittsburgh 17-10 1691.14 323 Ohio Valley Pennsylvania DI D-I 1565.97 125.18 0.08
32 2 Ohio 19-5 1671.08 287 Ohio Valley Ohio DI D-I 1352.61 318.5 0.24
36 4 Haverford/Bryn Mawr 22-7 1618.48 225 Ohio Valley Pennsylvania DIII D-III 1404.25 214.22 0.15
49 7 Kenyon 20-1 1498.7 339 Ohio Valley Ohio DIII D-III 1095.33 403.4 0.37
71 9 Carnegie Mellon 11-14 1278.34 197 Ohio Valley Pennsylvania DI D-I 1318.63 -40.23 -0.03
75 2 Penn State 13-17 1258.65 239 Ohio Valley Pennsylvania DI D-I 1347.02 -88.34 -0.07
81 1 Case Western Reserve 10-13 1200.8 245 Ohio Valley Ohio DI D-I 1249.37 -48.53 -0.04
98 4 Lehigh 15-17 1090.18 186 Ohio Valley Pennsylvania DIII D-III 1074.01 16.15 0.02
109 3 Temple 5-16 1021.02 241 Ohio Valley Pennsylvania DI D-I 1272.51 -251.45 -0.2
115 3 West Chester 4-16 950.96 263 Ohio Valley Pennsylvania DI D-I 1305.9 -354.93 -0.27
116 2 Cedarville 13-8 947.19 264 Ohio Valley Ohio DIII D-III 876.15 71.02 0.08
119 2 Swarthmore 13-11 939.18 256 Ohio Valley Pennsylvania DIII D-III 950.07 -10.9 -0.01
124 8 Cincinnati 12-12 911.96 283 Ohio Valley Ohio DI D-I 1011.9 -100.23 -0.1
155 31 Xavier 10-11 677.89 457 Ohio Valley Ohio DIII D-III 703.6 -25.68 -0.04
199 34 Oberlin 1-16 441.28 396 Ohio Valley Ohio DIII D-III 790.35 -349.04 -0.44
202 Messiah 1-3 396.88 Ohio Valley Pennsylvania DIII D-III 730.8 -333.95 -0.46
214 18 Dayton 4-8 269.87 324 Ohio Valley Ohio DI D-I 389.38 -119.2 -0.31
225 12 Dickinson 3-13 205.4 271 Ohio Valley Pennsylvania DIII D-III 451.26 -245.92 -0.54
236 27 Miami (Ohio) 2-8 109.99 391 Ohio Valley Ohio DI D-I 279.58 -169.35 -0.61
245 18 Pennsylvania-B 0-11 35.18 288 Ohio Valley Ohio Valley Dev Dev 635.11 -600 -0.94

FAQ

The results on this page ("USAU") are the results of an implementation of the USA Ultimate Top 20 algorithm, which is used to allocate post season bids to both colleg and club ultimate teams. The data was obtained by scraping USAU's score reporting website. Learn more about the algorithm here. TL;DR, here is the rating function. Every game a team plays gets a rating equal to the opponents rating +/- the score value. With all these data points, we iterate team ratings until convergence. There is also a rule for discounting blowout games (see next FAQ)
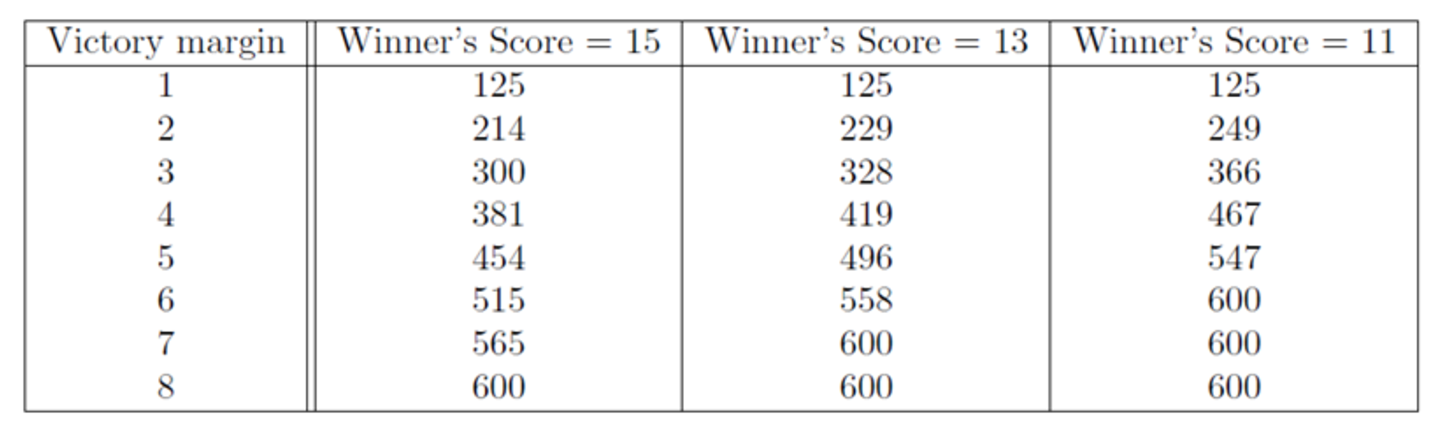
For reference, here is handy table with frequent game scrores and the resulting game value:
"...if a team is rated more than 600 points higher than its opponent, and wins with a score that is more than twice the losing score plus one, the game is ignored for ratings purposes. However, this is only done if the winning team has at least N other results that are not being ignored, where N=5."

Translation: if a team plays a game where even earning the max point win would hurt them, they can have the game ignored provided they win by enough and have suffficient unignored results.